Minimum Cost to Move Chips to The Same Position

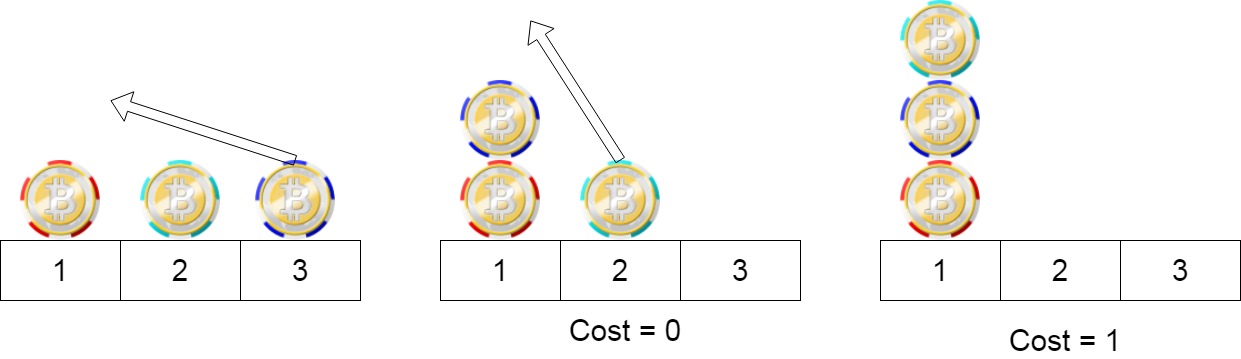
Minimum Cost to Move Chips to The Same Position题目大意：有n摞筹码，每个筹码可以以如下的方式移动：

• 以代价0向左或者向右移动2格
• 以代价1向左或者向右移动1格

求把所有筹码摞成一摞的最小代价。

根据题意，所有奇数位置的筹码可以无代价移动到奇数位置，偶数位置的筹码可以无代价移动到偶数位置，在奇数位置和偶数位置之间移动才需要代价，所以只需要统计奇数位置和偶数位置的筹码数量哪种比较多。

Convert Binary Number in a Linked List to Integer

Convert Binary Number in a Linked List to Integer题目大意：一个链表只包含0和1，把这个链表看作一个二进制数，求这个数的十进制表示。

略。

Binary Tree Tilt

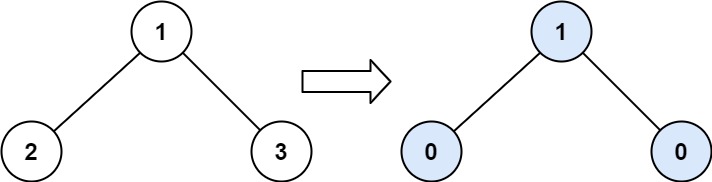
Binary Tree Tilt题目大意：求二叉树每个结点坡度之和。二叉树结点的坡度是该结点左子树结点之和与右子树结点之和的差的绝对值。

略。

Jump Game III

一个系列题目，一共有7道题，每道题之间的解法也不太一样。

Jump Game题目大意：已知一个数组nums，初始在第一个位置，每个位置的数字表示从这个位置最多可以跳多远，如果能到达最后一个位置，返回true，否则返回false。

模拟题，用range表示可抵达的范围，那么最初range=0。从0开始遍历所有下标小于等于range的位置，如果可以到达更远的位置就更新range，最后判断range是否包含最后一个位置。

Jump Game II题目大意：已知一个数组nums，初始在第一个位置，每个位置的数字表示从这个位置最多可以跳多远，求最少需要多少步可以跳到最后一个位置。题目保证可以跳到最后一个位置。

还是模拟，一步一步跳，每一个位置都有一个可以抵达的范围，在这个范围内找到跳得最远的位置作为下一步的落脚点，直到能够到达最后一个位置。

Jump Game III题目大意：已知一个数组nums，初始在位置start，每次从下标i可以跳到下标i-nums[i]或者i+nums[i]，求能不能从起始位置跳到一个值为0的位置。

按照题意进行深度优先搜索。

Jump Game IV题目大意：已知一个数组arr，初始在第一个位置，每次可以从下标i按照如下规则跳跃：

• 当i+1<arr.length时跳到i+1
• 当i-1>=0时跳到i-1
• 当arr[i]==arr[j]并且i!=j时跳到j

求最少多少步可以跳到最后一个位置。

需要定义几个数组，step[i]表示到下标i最少需要的步数，visited[i]表示是否到达过下标i。建立一个队列，每次找到能够到达的新的点就加入队列，这样可以保证队列里的下是按照到达步数递增排列的。建立一个hash表，对于数组中的每一个值，都记录数组里这个值的所有下标。

初始化step[0]=0,visited[0]=true，把0加入队列。循环遍历队列，从队列中取出第一个元素x，如果这个元素是最后一个位置就跳出循环。否则先判断x-1是否访问过，如果没有访问过，更新step[x-1]=step[x]+1,visited[x-1]=true，把x-1加入队列。然后对x+1做类似操作。接下来遍历hash[arr[x]]中的所有下标，更新其中未被访问过的下标的step和visited数组，并加入队列。遍历完成后清空hash[arr[x]]。（注意：一定要清空，这是为了避免重复遍历，我就是因为没有清空所有个别样例一直超时。）循环结束后step[arr.length-1]即为所求。

Jump Game V题目大意：已知一个数组arr和一个整数d，每次可以从下标i按照如下规则跳跃：

• 如果i+x<arr.length并且0<x<=d，可以跳到i+x
• 如果i-x>=0并且0<x<=d，可以跳到i-x

并且从i跳到j时必须满足arr[i]>arr[j]和i与j之间的所有下标k都满足arr[i]>arr[k]。

可以选择从任何位置开始跳跃，求最多可以访问多少个下标。

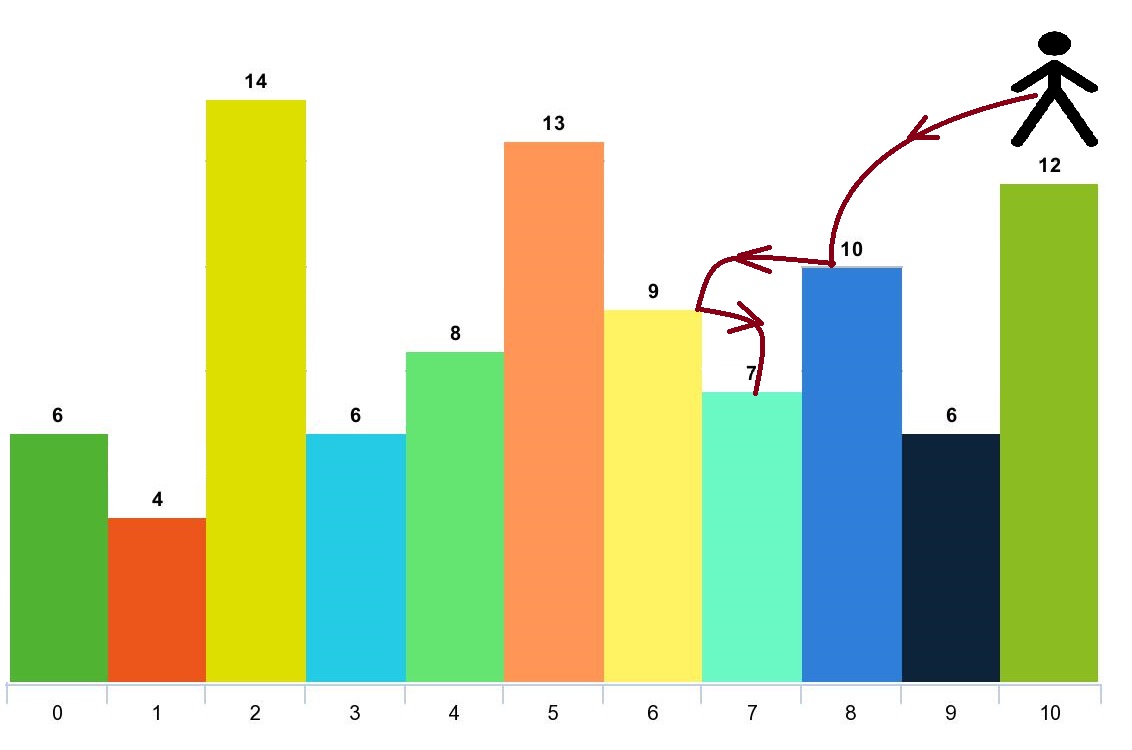
通俗地说就是只能从高处向低处跳，最远跳跃距离是d，并且途经的位置也必须比起点低。用dp[i]表示以下标为i的位置为起点最多可以访问多少下标。那么状态转移公式为：dp[i]=max(1,max(dp[j])+1)，其中j是从i可以跳到的下标。为了保证在计算dp[i]时所有dp[j]都已经被计算过，应该把所有下标按照高度从低到高排序，然后按照排序计算dp[i]。最后取所有dp[i]中最大的。

Jump Game VI题目大意：已知一个长度为n的整型数组nums和整数k，起始下标为0，每次可以从下标i跳跃到区间[i+1,min(n-1,i+k)]中的任意下标。当跳跃到数组的最后一个下标也就是n-1的时候，你的得分是途中经过的每个下标处值之和，求可能得到的最大得分。

用dp[i]表示在跳跃到下标i处时可以获得的最大得分，那么dp[i]=max(dp[j])+nums[i]，其中j是可以跳到i的下标。因为这道题的数据规模很大，$1 <= k <= 10^5$，所以需要一个能快速找到最大的dp[j]的方法。

维护一个最大优先队列，把所有计算过的dp[j]都放进去，计算dp[i]的时候就从队列头部取dp[j]，如果j不能跳到i就弹出，直到j能够跳到i，用dp[j]更新dp[i]。最后dp[n-1]即为所求。

Jump Game VII题目大意：已知一个字符串s和两个整数minJump和maxJump。起始下标为0，对应字符也是'0'。符合以下条件时可以从下标i跳跃到下标j：

• i+minJump <= j <= min(i+maxJump, s.length-1)
• s[j]=='0'

如果能跳跃到数组最后一个位置，返回true，否则返回false。

首先如果s[s.length-1]不是'0'可以直接返回false。其他情况我们就需要判断是不是真的能跳跃到最后一个下标。

每次从下标i可以跳跃到的范围是[i+minJump, min(i+maxJump, s.length-1)]，如果最后一个下标在这个范围内就可以返回true，否则我们需要记录这个范围内所有s[j]=='0'的下标j用于后续的跳跃。

用一个队列维护起跳位置，初始只有0，同时记录已经处理过的最大跳跃范围range。每次从队首弹出一个起跳位置i，那么从i跳跃范围的左边界l=i+minJump，右边界r=min(i+maxJump,s.length-1)。如果左边界l>s.length-1，那么返回false，因为从后续的位置只会跳得比i远，范围也不会包含最后一个下标。如果s.length-1在左右边界之间，返回true。都不是就说明还需要继续跳跃，首先更新l=max(l,range+1)，这是为了避免重复处理，只处理没有处理过的下标。把l和r之间所有为'0'的下标都加入队列，更新range=r。如果循环结束都没有返回，就说明跳得不够远，返回false。

Domino and Tromino Tiling

Domino and Tromino Tiling题目大意：求下面两种形状拼成2×n的形状有多少种方法。

例如拼成2×5的形状有以下方法：

这道题是真的没想明白，直接看大神推导的递推公式吧。看到下面的评论“高中一眼看出来的公式，现在一开始以为是魔法。”真的泪目了。

Nth Magical Number

Nth Magical Number题目大意：如果一个正整数能整除a或者b就称为魔数。已知n，a和b，求第n个魔数。

魔数是有一个周期的，也就是a和b的最小公倍数lcm。任何魔数加上最小公倍数的整数倍还是魔数。一个周期内的魔数有$N = lcm/a + lcm/b -1$个。那么第n个魔数就是lcm的$\lfloor n/N \rfloor$倍加上第$n\bmod N$个魔数。前者容易计算，后者可以把lcm以内所有a和b的倍数放到一个数组中排序求得。

还有一种纯数学方法是利用魔数的分布去逼近，然后求出准确值。我专门和数院的同学讨论了一下这种方法为什么能准确地求出第x个魔数，因为它通过近似找到了不小于第x个魔数的a的倍数和b的倍数，这两个数就是第x个和第x+1个魔数。

Partition Equal Subset Sum

Partition Equal Subset Sum题目大意：已知一个由正整数构成的非空集合，求能不能把它分成两个集合，这两个集合中数字的和相等。

这道题思路很简单，首先把集合中所有数字加起来，如果和是奇数那么肯定不可能，如果是偶数那么题目变成能不能在集合中找到一些整数加起来等于和的一半。

能够想到用动态规划来解，用dp[i][j]表示用nums[0]到nums[i]的集合能否找到和为j的子集。那么状态转移条件是，当选择nums[i]加入子集时，如果dp[i-1][j-nums[i]]==true，那么dp[i][j]=true。当不选择nums[i]加入子集时，如果dp[i][j]==true，那么dp[i][j]=true。

可以进行状态压缩，用dp[j]表示能否找到和为j的子集。遍历整个数组，对于每个下标i，从和的一半开始遍历j到nums[i]，如果dp[j-nums[i]]==true，那么dp[j]=true。