Accounts Merge

Accounts Merge题目大意：有很多组账户信息，账户信息包括用户的名字和该用户所拥有的一个或者多个邮箱。如果两个用户拥有同一个邮箱，就说明这两个用户是同一个人。两个用户的名字相同但是不拥有同一个邮箱则认为他们是名字相同的不同用户。把所有用户相同的账户信息合并，按照题目规定的格式输出。

用并查集解决，每个账户信息可以看作一个集合，如果两个集合中有公共的邮箱地址就合并。用一个hash表保存邮箱和集合之间的映射关系，方便快速找到出现相同邮箱的集合。

Maximal Rectangle

Maximal Rectangle题目大意：在由0和1构成的矩形中，找到最大的只由1构成的矩形，输出它的面积。

容易想到用动态规划解决，但是方法不太容易想。用dp[i][j]表示第i行第j列之前共有多少个连续的1。状态转移关系如下：

if (matrix[i][j] == 0)
{
    dp[i][j] = 0;
}
else
{
    if (j == 0)
    {
        dp[i][j] = 1;
    }
    else
    {
        dp[i][j] = dp[i][j-1] + 1;
    }
}

遍历所有的坐标(i,j)，遍历所有在[i,matrix.size())之间的k，计算右上为(i,j)右下为(k,j)的最大矩形面积并更新答案。这样的矩形一边长度为(k-i+1)，另一边的长度为从i到k所有dp[i][j]的最小值。

House Robber

House Robber题目大意：你是一个专业的抢劫犯准备沿着一条街抢劫，已知一个数组表示这条街上每一家可以抢劫到的钱数。如果街上相邻两家被抢就会自动报警，求在不触发警报的情况下最多可以抢到多少钱。

一道动态规划的题目。用dp[i]表示抢劫第i家时最多可以抢到多少钱，状态转移关系如下：

dp[i] = nums[i];
if (i > 1)
{
	dp[i] = nums[i]+dp[i - 2];
}
if (i > 2)
{
	dp[i] = max(dp[i],nums[i] + dp[i - 3]);
}

至少可以保证抢到第i家的钱，如果i足够大，在不触发警报的情况下考虑前面的抢劫，只有两种情况，上一次抢劫的是第i-2家或者是第i-3家。在这几种情况中选择钱最多的更新dp[i]，并用dp[i]更新答案。

Odd Even Linked List

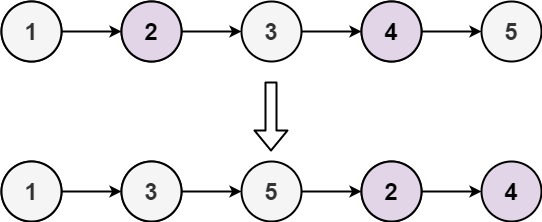
Odd Even Linked List题目大意：把链表中的奇数结点和偶数结点各自组织成一个链表并连接。

考察基本的链表操作，定义奇链表和偶链表，遍历初始链表，按照奇偶把结点加入这两个链表中，最后把偶链表连接在奇链表后面。

Maximum Product Subarray

Maximum Product Subarray题目大意：求一个数组的乘积最大的子数组，返回乘积的值。子数组是指数组中连续的一部分。

之前做过的Maximum Subarray是求和最大的子数组，这道题和它类似，区别在于最大乘积存在负负得正的情况，因此不能简单维护一个数组。维护两个数组pos[i]和neg[i]，分别表示以i为结尾的子数组乘积的最大值和最小值。状态转移关系取决于nums[i]的正负：

if (nums[i] >= 0)
{
	pos[i] = max(nums[i], pos[i - 1] * nums[i]);
	neg[i] = min(nums[i], neg[i - 1] * nums[i]);
}
else
{
	pos[i] = max(nums[i], neg[i - 1] * nums[i]);	
	neg[i] = min(nums[i], pos[i - 1] * nums[i]);
}

最大的pos[i]就是答案。

Stream of Characters

Stream of Characters题目大意：已知一个字典，实现一个类，该类每次从字符流中读取一个字符并能够判断字符流的后缀是否出现了字典中的单词。

这道题用到的数据结构是Trie树，也叫做字典树，同样是之前听说过但是没有用过的。这种数据类型能够把字典储存在一棵树中，最基本的应用是查找一个字符串是否在字典中出现。在这道题中是查找字符串的后缀是否在字典中出现。

通常来说字典树可以用来查找字符串的前缀是否在字典中出现，要查找字符串的后缀是否在字典中出现就需要倒序建树并且倒序查找。

House Robber III

House Robber系列题型，一共包含三道题。

House Robber上面已经讲过，就不再赘述。

House Robber II题目大意：条件和第一题相同，区别在于街道变成了首尾相连。

这道题在第一题算法的基础上修改一下就可以，我把情况分成了抢劫第一家和不抢劫第一家，想了很久都没有做出来。实际上首尾相连之后第一家和最后一家不能被同时抢劫了，在数组中分别删除第一项和删除最后一项，用第一题的算法各算一遍取最大的结果即可。

House Robber III题目大意：这道题住宅区从线性变成了树形，劫匪要抢劫形如二叉树的区域，如果抢劫直接相连的两家就会触发警报，求在不触发警报的情况下最多可以抢劫到多少钱。

还是用动态规划，递归地为每个结点计算两个数值rob和notRob，分别表示在当前结点抢劫和不抢劫所能获得的最大金钱。如果结点为空，那么这两个数值都为0。如果结点不为空，那么当前结点的状态转移公式如下：

root->notRob = max(root->left->notRob,root->left->rob) + max(root->right->notRob,root->right->rob);
root->rob = root->left->notRob + root->right->notRob + root->val;

取根结点的rob和notRob的最大值就是答案。