Delete Node in a BST

Delete Node in a BST题目大意:删除二叉搜索树的一个结点。
数据结构与算法的经典问题,分三种情况:
- 该结点是叶子结点,直接删除;
- 该结点只有一个子结点,用子结点代替该结点位置;
- 该结点有两个子结点,删除该结点后,为了保持二叉搜索树的性质,应该用左子树的最大值或者右子树的最小值代替该结点。
可以参考OI Wiki。
Largest Component Size by Common Factor

Largest Component Size by Common Factor题目大意:已知一个由不同正整数构成的数组,按照如下规则构造一个无向图:
- 数组中的每个数都代表图中的一个顶点;
- 如果两个数存在大于1的公约数,则这两个数代表的顶点之间存在一条边。
求该图的最大连通分支中包含多少个顶点。
这道题其实不是图论问题,而是集合划分问题,按照不同的连通分支把数组中的数划分为不同的集合,求最大的集合里有多少个数。解决这类问题用到的数据结构是并查集,并查集能够用来处理一些互不相交的集合的合并和查询的问题。并查集的定义和实现可以参考OI Wiki。
首先需要给顶点划分集合,如果两个数存在1以外的公约数就应该把它们所在的集合合并,但是对每个数都去求它和其他所有数有没有公约数包含了很多重复的工作量。不妨换一种思路,如果我们把每个数和它的所有非1约数的集合都合并,那么两个有非1公约数的数就都跟这个公约数在同一个集合里。然后对每个顶点查找它在哪一个集合里,更新集合的大小和答案即可。
Interval List Intersections
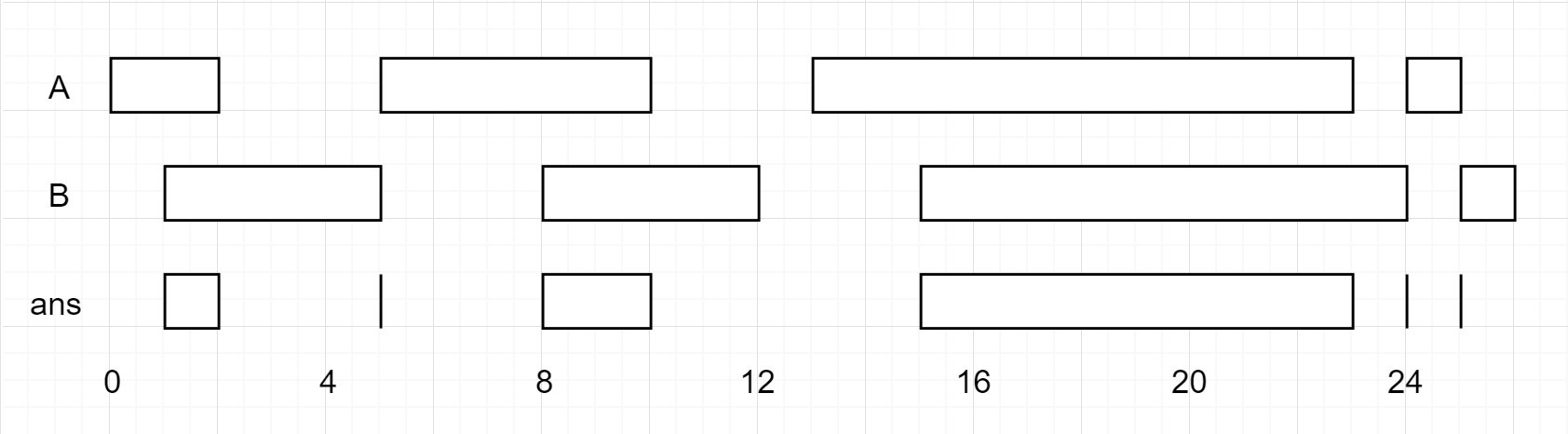
Interval List Intersections题目大意:已知两个数组,其中包含的是互不相交并且有序的闭区间,求这两个数组中区间的交集。
这道题是贪心法的一个典型应用。对数组A和B分别维护下标i和j,i和j初始化为0。计算区间A[i]和B[j]的交集,交集的左边界是max(A[i][0],B[j][0]),右边界是min(A[i][1],B[j][1]),如果左边界大于右边界说明交集为空。然后比较两个区间的右边界,保留右边界较大的区间,将另一个区间的下标加1。如果两个区间的右边界相等,则两个下标都加1。
Maximum Subarray
Maximum Subarray题目大意:求一个数组的和最大的子数组,返回和的值。子数组是指数组中连续的一部分。
这道题是典型的动态规划问题。用dp[i]表示以下标i结尾的子数组的和的最大值,那么有两种可能,一种是nums[i]自己构成一个子数组,另一种是它和前面的若干数构成一个子数组,这些子数组中和最大的是以下标i-1结尾的和最大的子数组再加上nums[i],所以状态转移公式是dp[i]=max(nums[i],dp[i-1]+nums[i])。初始条件是dp[0]=nums[0]。
Search Insert Position
Search Insert Position题目大意:已知一个包含各不相同的整数的有序数组中和一个目标值,如果能在数组中找到目标值就返回它的下标,如果不能找到就返回它插入数组中并保持数组有序时它的下标。算法时间复杂度应为。
看题意就知道应该用二分法,需要注意最后找不到目标数时应该返回什么下标。
Product of Array Except Self
Product of Array Except Self题目大意:已知一个整型数组nums,求数组answer,使得answer[i]的值是nums中除nums[i]以外所有值之积。题目要求算法复杂度为并且不使用除法。
自然的想法肯定是把所有数相乘然后依次除以每一个数即可,但是因为数组中可能包含0,所以这种方法本来也行不通。换一种思路,用pre[i]表示下标小于i的所有数的乘积,用post[i]表示下标大于i的所有数的乘积,那么answer[i]=pre[i]*post[i],而求pre[i]和post[i]也只需要把数组正反各扫描一遍。
All Paths From Source to Target

All Paths From Source to Target题目大意:已知一个包含n个顶点的有向无环图,求从0号顶点到n-1号顶点的所有路径。
使用深度优先搜索即可,在搜索时记录路径,只要到达n-1号顶点就把路径加入答案。
