Largest Divisible Subset

Largest Divisible Subset题目大意：已知一个不同正整数组成的集合nums，求它的一个最大子集合answer，answer中任意两个整数都满足其中一个是另外一个的整数倍。

这道题和动态规划的经典问题Longest Increasing Subsequence类似，只是把条件从大小关系变成了整除关系。

因为只可能较大的数整除较小的数，所以要先把nums从小到大排序。接下来找到nums的满足sub[i+1]%sub[i]==0最大子序列sub就得到了答案，因为sub具有其中任意一个整数都能整除sub中比它小的整数并且被sub中比它大的整数整除的性质。

用dp[i]存储包含nums[i]的最大子序列sub的长度，用pred[i]存储在该子序列中nums[i]的前驱在nums中的下标。对所有i<j，当nums[j]%nums[i]==0 && dp[i]+1>dp[j]时更新dp[j]=dp[i]+1; pred[j]=i。最后根据dp找到最大的子序列和其中最大的元素，再根据pred找到所有其他元素。

Kth Smallest Number in Multiplication Table

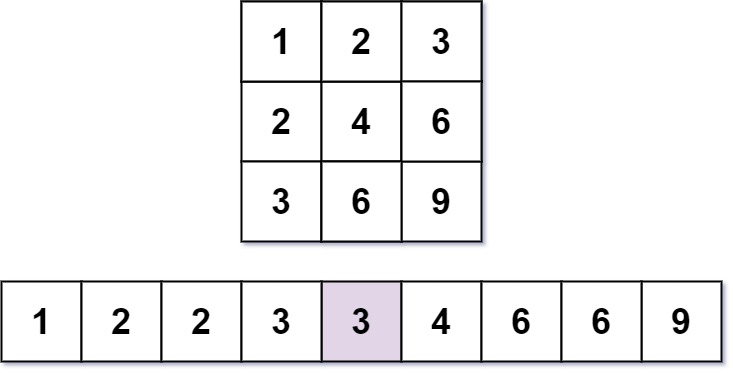
Kth Smallest Number in Multiplication Table题目大意：求乘法表里第k小的数。乘法表是一个矩形表格，其中每一格中的数是这一格的行号乘列号。

又一道题意简单但是数据规模庞大的题。这道题可以使用二分查找来降低时间复杂度，找到乘法表在1~x区间内有至少k个数的最小x即可。

假设乘法表大小为m×n，初始化二分查找的左边界l=1，右边界r=m*n。查找时首先计算中点mid=(l+r)/2，然后计算乘法表在1到mid之间有多少数，如果有不少于k个，说明应该缩小区间，r=mid；如果不足k个，说明应该扩大区间，l=mid+1。左右边界相等时就找到了要求的x。二分查找算法模板参见AcWing。

由于乘法表每一行都是行号的倍数，第i行就有min(n, mid/i)个数在1和mid之间，遍历每一行就可以知道乘法表中一共有多少数在1和mid之间。

Unique Paths

这道题在LeetCode 每日一题周总结 (一)中讲到过。

Find All Numbers Disappeared in an Array

Find All Numbers Disappeared in an Array题目大意：已知一个数组大小为n，其中包含1到n之间的整数，求1到n之间有哪些整数没有在数组中出现。

数组大小为n，其中包含的整数也在1到n之间，那么可以把数组中的整数放到对应下标的位置上去，最后遍历数组，对应下标上的数字不正确就表示缺少这个整数。

思路很简单，但是编码过程中有不少细节。遍历数组到下标i，nums[i]对应的下标是nums[i]-1，首先检查nums[nums[i]-1]是否和nums[i]相等，如果相等就说明那个下标已经有对应的数字了，继续遍历；如果不相等就交换nums[i]和nums[nums[i]-1]，交换后nums[i]是原先在nums[nums[i]-1]处的数字，需要重新判断是否需要交换，这时需要把下标i减1，确保下次遍历还检查nums[i]。

Hamming Distance

Hamming Distance题目大意：求两个整数的汉明距离。两个整数之间的汉明距离指的是这两个数字对应二进制位不同的位置的数目。

把两个整数异或，计算结果的二进制表示中有多少位为1即可。

Single Element in a Sorted Array

Single Element in a Sorted Array题目大意：在有序数组中有一个元素只出现一次，其余元素均成对出现，找到这个只出现一次的元素。要求时间复杂度为$O(\log n)$，空间复杂度为$O(1)$。

如果没有附加条件，这道题可以直接使用Single Number的方法求解。考虑到附加条件和已知数组有序，应该使用二分查找来求解。

二分查找的关键是如何判断这个元素在左半边还是在右半边。如果没有这个元素，那么成对元素的下标应该是2n和2n+1，但是这个元素出现后，成对元素的下标就会向后偏移一位。首先确定中点下标mid，找到和mid组成(2n,2n+1)对的另一个下标，可以对mid的奇偶分类讨论，还有一种简单的方法，另一个下标是mid异或1。然后判断这两个下标对应的元素是否相等，相等就说明要找的元素还没出现，在右半边；不相等就说明要找的元素在左半边。

Construct Binary Tree from Inorder and Postorder Traversal

Construct Binary Tree from Inorder and Postorder Traversal题目大意：已知一棵树的中序遍历和后序遍历，构造出这棵树。题目保证中序遍历和后序遍历的数都唯一出现。上图为用中序遍历[9, 3, 15, 20, 7]和[9, 15, 7, 20, 3]构造的二叉树。

可以先建立根结点，再递归地构造左子树和右子树。根结点的值是后序遍历的最后一个值，在中序遍历中找到这个值，以它为分界点把中序遍历分成左右两部分，左半边是左子树的中序遍历，右半边是右子树的中序遍历。这样就得到了左右子树的大小，根据左右子树的大小可以从后序遍历中提取出左子树的后序遍历和右子树的后序遍历。用根结点的值建立根结点，递归调用函数，用左子树的中序遍历和后序遍历生成左子树，并赋值给根结点的指针，然后再类似地生成右子树赋值给根结点的指针。最后返回根结点。

注意边界条件，如果中序遍历和后序遍历为空，返回空指针。